Paseando entre rectángulos áureos

Hoy, junto a mis estalmateros palmeros, pasearíamos por las calles de Santa Cruz de La Palma para unir patrimonio y geometría.

Desgraciadamente, en esta ocasión, el paseo será virtual. En este recorrido tendremos que resolver acertijos, buscar polígonos cóncavos, rectángulos áureos y rombos laguneros. Para, para,…me acabo de perder.
Tenéis razón, debemos introducir unos pequeños conceptos:
Rectángulo áureo y el test de Paula
Hay infinitos tipos de rectángulos porque sus lados pueden estar en infinitas proporciones. Pues bien, entre todos ellos hay uno que se conoce como rectángulo áureo. Se llama así porque sus lados están en la proporción áurea. Dicha proporción significa que si dividimos el lado mayor entre el lado menor nos da el número áureo Φ= 1,618.
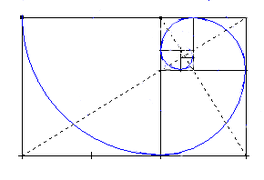
Por tanto, para saber si un rectángulo es áureo basta con medir sus lados y calcular el cociente, pero no es la única forma ya que el rectángulo puede ser no accesible.
En ese caso, toma en tus manos la tarjeta áurea que te hemos entregado virtualmente (sirve también el DNI). Si desean saber si, por ejemplo, una ventana tiene proporción áurea, situar la tarjeta entre el ojo y la ventana, acercando o alejando el brazo, tratando de conseguir que el rectángulo que está en la mano coincida con el de la ventana. Será áureo si se consigue encajar (“Test de Paula”).
Rombo lagunero
Es aquel en el que la diagonal mayor D mide el doble que la diagonal menor d. ¿Seremos capaces de encontrar un rombo lagunero palmero?
Polígono cóncavo
Es el polígono que tiene al menos un ángulo interior de más de 180º ( si todos son menores de 180º es convexo).
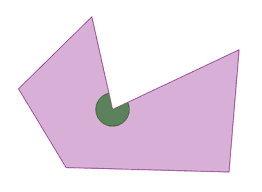
Y ya provistos de conocimientos y de nuestro cuadernillo virtual junto a nuestra tarjeta áurea, la cinta métrica y, sobre todo, mucha ilusión matemática nos lanzamos a resolver los retos planteados mientras buscamos polígonos cóncavos, rectángulos áureos y rombos laguneros por las calles de Santa Cruz de La Palma. Comparto alguno de ellos:
Y como en algún lugar dicen que debemos empezar.

El barco tiene un papel muy importante en la Bajada Lustral de la Virgen de las Nieves. Cuando la Virgen llega junto al barco tiene lugar el “Diálogo entre el Castillo y la Nave”. Es un acto, obra del poeta Antonio Rodríguez, estrenado en las Fiestas Lustrales del año 1875 y que se representa de manera ininterrumpida desde 1885 como homenaje al pasado naval de la isla y al patronazgo marinero de la Virgen.
¿Con los datos aportados cuántas veces ha tenido lugar ese singular diálogo? Además indica 6 elementos geométricos que aprecies en el barco.
Casi al lado del Barco de la Virgen, nos encontramos una casa numerada con un número 6. Y la parada no ha sido casual.
Según los pitagóricos, el 6 es un número perfecto pues es igual a la suma de sus divisores, excluyendo el 6, claro.
\textcolor{red}{6=1+2+3}¿Cuál es el siguiente número perfecto?
Concluimos nuestro paseo matemático en otro lugar emblemático de nuestra ciudad.

La espadaña de la Plaza de España está coronada por un reloj de agujas. Indicar cuánto mide el ángulo que forman las dos agujas en las horas siguientes:
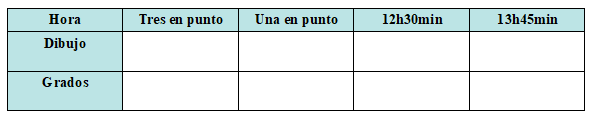
Y tras este recorrido geométrico, cae la noche en estos días tan especiales que nos han tocado vivir.

Y para terminar, agradecer a José Carlos Martín Díaz, gran fotógrafo y amigo, por dar “color” a esta entrada.




Tres en punto:
agudo
Una en punto:
agudo
12h30m:
llano
13h45m
obtuso
Buenas.. Debes ser más preciso y decir los grados exactos.. Además cuando son las 12 y media, la aguja de las doce está quieta en el 12 o se ha movido un poco…
EL DIALOGO ENTRE EL CASTILLO Y LA NAVE SE HA REALIZADO 28 VECES.
EL SIGUIENTE NUMERO PERFECTO ES EL 28 = 1 + 2 + 4 + 7 + 14.
A LAS TRES EN PUNTO SE PRODUCE UN ANGULO RECTO (90º).
A LA UNA EN PUNTO SE PRODUCE UN ANGULO AGUDO DE 40º.
A LAS DOCE Y MEDIA SE PRODUCE UN ANGULO OBTUSO DE 173º.
A LAS DOS MENOS CUARTO SE PRODUCE UN ANGULO OBTUSO DE 140º.
Hola yo creo que el numero de diálogos es de 27, 1 en 1875 y 26 mas desde 1885 hasta 2015 que fue la ultima.
En el barco veo círculos, rectángulos, triángulos, polígonos irregulares, polígonos regulares y cuadrados.
El siguiente número perfecto es el 28 = 1+2+4+7+14.
Las 3 en punto forman un ángulo recto, 90º
La 1 en punto forma un ángulo agudo de 60º
Las 12:30 forma un ángulo llano de 180º
Y las 13:45 forma un ángulo obtuso de 145º
Buenas.. Respecto al reloj,, seguro que a la 1 son 60 grados? Si a las tres dices que son 90 grados.. Y las dos últimas horas pues sería correcto si la aguja de las horas se quedará quieta… Te invito a mirar un reloj y ver si a las 18.30 o 19.30 la aguja de las horas se ha movido.. Un saludo y buen trabajo
Se han realizado el dialogo 28 veces
El siguiente numero perfecto es 28 = 1 + 2 + 4 + 7 + 14.
A las tres en punto es un angulo recto (90 grados)
A la una en punto es un angulo agudo (40 grados)
A las doce y media es un angulo obtuso (170 grados)
A las dos menos cuarto es un angulo obtuso (140 grados)
Buenas.. Si a las 3 son 90 grados a la una seguro que son 40 grados?