!!!Cuadros en cuadro!!!

Inauguramos nueva sección en el rincón matemático de Sherlock: “Actividades Estalmat” . ¡¡¡Comenzamos!!!.
Hoy quiero presentaros al pintor holandés Piet Mondrian (1872-1944).
Dentro de su obra pictórica, nos vamos a detener en el cuadro de 1921 “Composición en rojo, amarillo y azul” . Obra que es una de las máximas expresiones y representaciones del arte abstracto moderno.

Asociado a esta obra, nos encontramos con el problema matemático de Mondrian. Éste consiste en dividir una cuadrícula de dimensiones n x n, en rectángulos y cuadrados de lados enteros e incongruentes entre sí (es decir, que no haya dos iguales), de tal modo que la diferencia entre la superficie del rectángulo mayor y el menor sea la menor posible. Esa resta dará la puntuación y el objetivo final es minimizarla.
Quizás lo veamos mejor con un ejemplo. Consideremos la cuadrícula de 4×4 y dentro de las posibilidades que tenemos, una de ella es la siguiente:
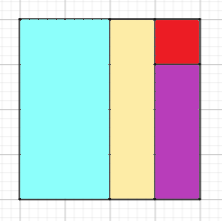
El paso siguiente será calcular las áreas de los rectángulos/cuadrados dibujados (recordar que sus medidas deben ser enteras y que deben ser diferentes).
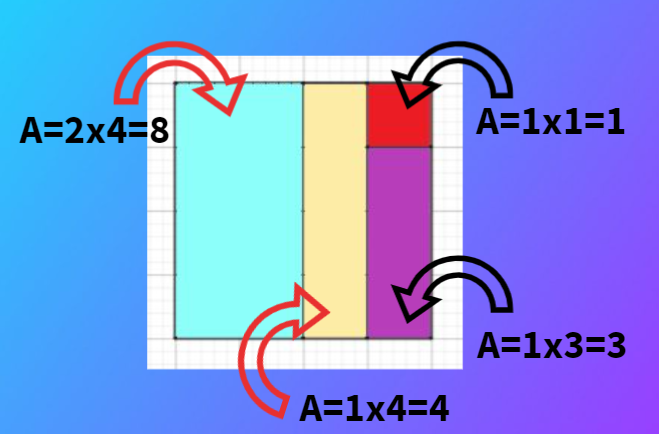
Por último, calcularemos la puntuación asociada.
Y es aquí donde debemos empezar a pensar. ¿Serás capaz de encontrar la puntuación mínima en el caso de 4×4? ¿Y en 5×5, 6×6, 7×7 y 8×8?…Pues lo dicho, ¡¡¡a pensar!!!.



