Irracionalmente bello

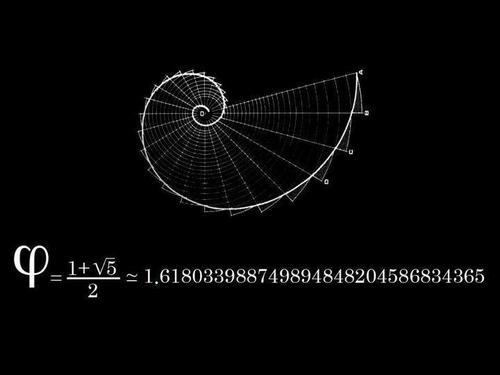
¿Qué tiene que ver esta tarjeta con las matemáticas? Seguramente podríamos dar muchas respuestas pero la que buscamos viene dada por sus dimensiones.

Y en este resultado tenemos la respuesta: el número Phi φ, número áureo, número de oro o divina proporción.

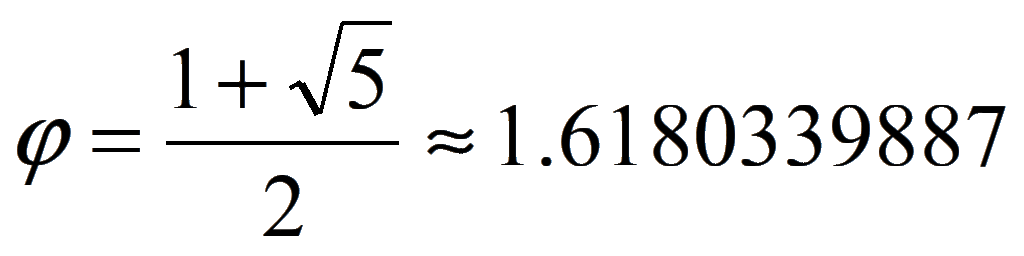
¿Qué sabemos de φ ? Fue un hallazgo de los griegos de la época clásica y su historia documentada comienza en uno de los libros más célebres de la historia: “los Elementos de Geometría de Euclides”, escrito alrededor del 300 aC y llamado “fi” en honor al famoso escultor griego Fidias (siglo 5 aC) que lo usó en sus obras.

Además como su buen amigo π, estamos ante un número irracional con infinitas cifras decimales y el símbolo φ se lo adjudicó en el año 1900 el matemático Mark Barr.

Y asociado a este número de oro se encuentra el rectángulo de oro o áureo, un rectángulo con una relación de longitud lateral de 1.618:1 ( si dividimos el lado mayor entre el lado menor nos da φ)

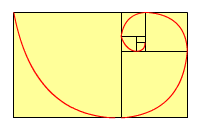
Este tipo de proporción rectangular se halla presente en multitud de obras arquitectónicas como el Partenón griego, las pirámides, la sede de la ONU, la catedral de Nôtre Dame.

También lo encontraremos en cuadros tales como “La Gioconda” y “El hombre de Vitruvio” de Leonardo da Vinci.

Otros artistas que hicieron uso del número áureo en sus obras fueron, por ejemplo, Sandro Botticelli, Charles Édouard Jeanneret-Gris (“Le Corbusier”), Salvador Dalí y Paul Klee.

Pero vamos a volver a Da Vinci y a su hombre de Vitruvio.

Vitruvio fue un destacado arquitecto romano del siglo I aC, quién publicó un tratado de arquitectura, escrito entre el 27 y el 23 aC. En dicho tratado, Vitruvio hacía mención de las proporciones que consideraba “ideales” para la figura humana.

Inspirado al leer una reedición del tratado, Leonardo da Vinci se dispuso a hacer su propia versión (1490) de aquél humano idealizado que Vitruvio describió.

Esta obra fue un reto da Vinci pero teminó realizando una muy fiel reproducción a lo descrito por Vitruvio. A pesar de ésto, hay muchos detractores que dicen que el dibujo no cumple con los parámetros de la razón áurea ya que la razón áurea de esta ilustración es igual a 1.642. 

Pero volviendo a la idea de Vitruvio, ¿seremos matemáticamente perfectos?. Para comprobarlo deberemos tomar las dos medidas siguientes: nuestra altura y la altura desde los pies al ombligo.

Y ya sólo me queda invitarte a que provisto de una cinta métrica, compruebes si matemáticamente te acercas a la belleza.