Soñando con puentes
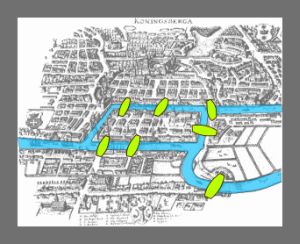
Suena el despertador y salgo de un extraño sueño. En él, viajaba al siglo XVIII y a la ciudad de Königsberg (actualmente Kaliningrado).
En el sueño escuchaba una discusión entre dos personas sobre el famoso problema de los puentes de Königsberg(creo que una de ellas era Christian Goldbach) sobre si se podría recorrer la ciudad, que es atravesada por el río Pregel que la divide en 4 zonas y que cuenta con siete puentes, sin pasar más de una vez por cada puente y terminando en el punto de salida.
Debo reconocer que la curiosidad me pudo y decidí intentar el reto planteado. Debo reconocer que fui incapaz de lograrlo.
Ahora bien despierto me planteo si realmente es imposible realizar dicho recorrido sin pasar más de una vez por cada puente siendo el punto de inicio y de llegada el mismo.
Este problema fue resuelto por Leonhard Euler en 1736 y se considera este problema el inicio de la teoría de grafos.

Se trata del principal matemático del siglo XVIII y uno de los más grandes de todos los tiempos. Realizó importantes descubrimientos en áreas tan diversas como el cálculo o la teoría de grafos. También introdujo gran parte de la moderna terminología y notación matemática, particularmente para el área del análisis matemático. También realizó contribuciones en los campos de la astronomía, la óptica y la mecánica.
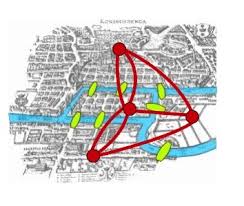
Para resolver el problema, Euler representó la ciudad de Königsberg como un grafo donde las cuatro partes de la ciudad eran los vértices o nodos (puntos) y los puentes eran las aristas (líneas que unen los vértices)
Por tanto, el problema sería recorrer el siguiente grafo sin pasar dos veces por la misma arista y que el vértice de salida sea el mismo donde terminamos.
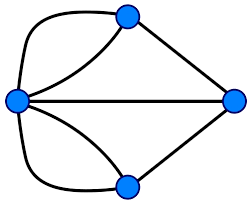
Te invito a intentarlo pero tampoco mucho rato ya que Euler demostró que era imposible. ¿Dónde está la clave para saber que es imposible?
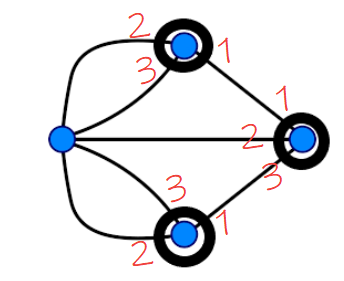
Debemos fijarnos en los vértices y contar las aristas o caminos que salen de cada vértice. Para poder recorrer este grafo, los vértices “intermedios” deben tener un número par de aristas(un camino para entrar y otro para salir). Sólo los vértices de inicio y salida pueden tener un número impar de aristas. De esta forma, podríamos salir de uno de esos vértices y terminar en el otro. Si además deseamos que el inicio y el final sean el mismo no puede existir ningún vértice del que salgan un número impar de aristas.
Si nos fijamos en el grafo de Euler, vemos que hay, al menos, tres vértices con un número impar de aristas. Por tanto, el famoso problema de los puentes de Königsberg es imposible. No existe un camino para recorrer este grafo y, mucho menos, para que el vértice inicial sea también el final.
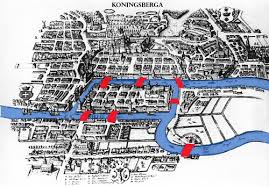
Como anécdota, comentar que en la II Guerra Mundial se destruyeron dos puentes y el problema ya no era imposible. Ya podemos realizar ese “paseo por los puentes de Königsberg”(con inicio y final diferentes). ¿Qué puentes crees que fueron destruidos? ¿Hay más de una opción?

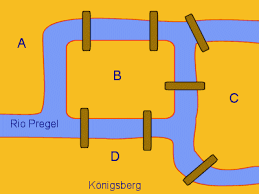



En las opciones que elegí pueden ser destruidos el puente central y el puente que está más arriba o el central y el que está más abajo. Se realiza (por ejemplo en la primera) caminando por los puentes izquierdos desde la D hasta la A y volviendo por los derechos de estos mismos, ya pasando por la D,A y B. Y finalmente caminando por el puente de abajo de la C y e el otro caso sería prácticamente lo mismo pero empezando desde la A hasta la D y volviendo a la A y al final por el puente de arriba de la C.
Creo que los 2 puentes destruidos son los laterales de la C.
Un saludo.
HOLA YO CREO QUE LOS DOS PUENTES DESTRUIDOS FUERON LOS DOS PUENTES ,AS ARRIBAS SITUADOS A LA DERECHA EN EL PUNTO C
UN SALUDO
Hola yo creo que fueron destruidos los dos puentes de arriba situado en el lado A