Teorema de los… colores

Vamos a dejar un poco de intriga y no vamos a desvelar la respuesta.
¿Cuántos colores necesitaríamos para pintar cualquier dibujo, mapa con la única condición que si dos regiones comparten frontera deben ser pintados con colores diferentes? Suponemos que si sólo comparten un punto si pueden ser pintados con el mismo color.
Vamos a empezar con un dibujo muy sencillo.
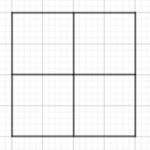

Manteniendo la misma estructura podíamos partir el cuadrado en 4 regiones para tener que usar 4 colores.
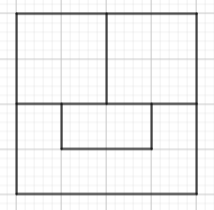
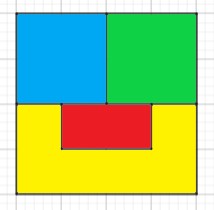
Podríamos suponer que si con sólo 4 regiones hemos necesitado 4 colores, si las regiones aumentan y fuesen 100,1000,1000000 debería aumentar el número de colores utilizados….Pues aquí está la respuesta:
“Nunca vamos a necesitar más de 4 colores” Podrá ser complicado lograrlo pero cualquier dibujo/mapa con la condición puesta puede ser pintado únicamente con 4 colores. Fue demostrado por K. Appel y W. Haken en 1976.
Un ejemplo :
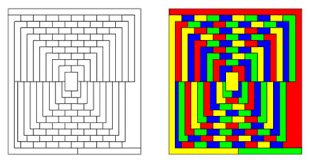
Por último, una explicación del gran Eduardo Sáenz de Cabezón




Buenas. Por cierto, ese año fue un año de grandes, diría grandísimos matemáticos canarios
Eso es conjetura o ya teorema??