¡¡¡Amigos eternos!!!

En estos tiempos donde empezamos de nuevo a sociabilizar (de manera segura, espero) quiero hablar de la amistad entre números. ¿En serio?. Pues sí, hoy hablaremos de números amigos.

Dos números amigos son dos números enteros positivos a y b tales que la suma de los divisores propios de uno es igual al otro número y viceversa (la unidad se considera divisor propio, pero no lo es el mismo número).

Veremos como ejemplo, la pareja de números amigos más pequeña y “famosa” que existe (220 y 284).

Divisores propios de 220 son:

Divisores propios de 284 son:

Este par de números amigos (220, 284) ya era conocido por los pitagóricos, quienes les atribuían propiedades místicas.

Como anécdota contaré una leyenda:

Cuenta una leyenda que había un sultán aficionado a los puzzles, que al descubrir que tenía a un matemático como prisionero, decidió plantearle la siguiente cuestión.

El sultán le dijo al matemático que le planteara un reto y que estaría libre durante el tiempo que él necesitara para resolverlo, pero una vez resuelto por el sultán, el matemático sería ejecutado.

El matemático le explicó que los números 220 y 284 son números amigos, y le planteó que buscara otro par de números amigos. El sultán no lo consiguió y el matemático murió de viejo y siendo un hombre libre.

De hecho, calcular más pares de números amigos no es fácil. Muchos matemáticos árabes estudiaron los números amigos como el iraquí Thabit ibn Qurra (826-901) quien dio una fórmula para obtener números amigos.

En particular, obtuvo tres nuevos pares de números amigos:

Grandes matemáticos (Fermat, Descartes, Euler,…) estudiaron los números amigos pero, cabe destacar, que hasta 1946 solo se consiguieron descubrir 390 pares de números amigos.

La aparición de los ordenadores y su potencia de cálculo, que junto a nuevos algoritmos, ha permitido calcular muchas parejas de números amigos pero sin embargo, no se sabe si existen infinitos pares de números amigos.

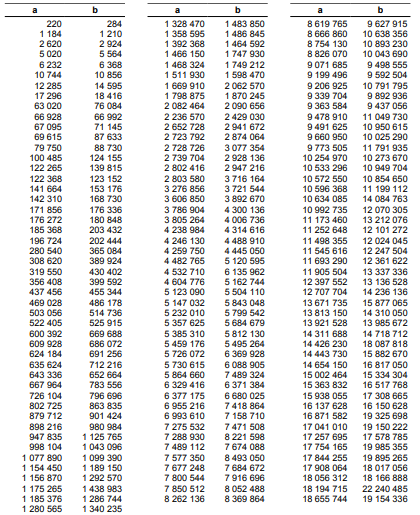
Te podría invitar a que compruebes la amistad de alguna de estas parejas de números amigos pero prefiero que cuides a tus amigos como hace el 220 con su querido 284.