La conjetura que sueña ser teorema
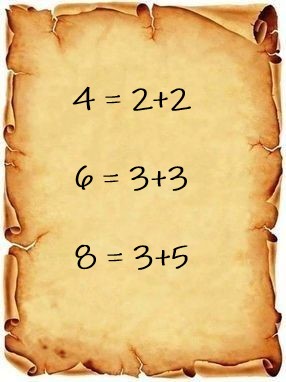
Un número primo es todo número natural mayor que 1 que únicamente tiene dos divisores (la unidad y el propio número). Por ejemplo, el siete es un número primo pues sólo tiene dos divisores (el 1 y el 7). Una vez puestos en situación, acabamos de ver el fragmento inicial de “La habitación de Fermat”, película español de 2007 dirigida por Luis Piedrahita y Rodrigo Sopeña. Esta película trata sobre la búsqueda de la demostración de la conjetura de Goldbach acompañada de acertijos matemáticos.

Christian Goldbach fue un matemático prusiano nacido en Konigsberg (otro día hablaremos de los puentes de esta ciudad) y se le considera uno de los matemáticos más influyentes del siglo XVIII. Creció en contacto con grandes matemáticos como Leibniz, los hermanos Bernoulli y sobre todo con Leonard Euler.
Justamente en una carta enviada a Euler en 1742 se nos presenta la conjetura de Goldbach: “Todo número par mayor que 2 se puede expresar como la suma de dos números primos”. Y aquí encontramos una pequeña errata en la escena que da pie a esta entrada.
Con números pequeños es fácil comprobar que es cierta y puede existir más de una combinación posible. Por ejemplo:
12 = 5+7
30 = 17+13
50 = 37+13
90 = 83+7
Pero, ese maldito pero, casi 300 años después, sigue sin demostrarse si esta conjetura es cierta o falsa.
Para demostrar que es falsa bastaría encontrar un número par mayor que 2 que no puede ser expresado como la suma de dos números primos. Por ahora ese contraejemplo no ha sido encontrado y, por ejemplo, Tomás Oliveira e Silva ha demostrado que la conjetura funciona con todos los números pares menores que 4000000000000000000, aunque no es suficiente para demostrar que es cierta.
Por contra, para demostrar que es cierta se debería encontrar una demostración o ley que incluyese a todos los números pares mayores que 2.
A día de hoy, el matemático australiano Terence Tao ha realizado grandes avances en la búsqueda de esta demostración que lleva escondida casi 300 años y ojalá que pronto la bella conjetura de Goldbach sea un teorema.



300= 283+17
100= 29+71
Muy bien
42=29+13
14=11+3
20=17+3
Buen trabajo